

You can also interpret this as the signal being made up of a sum of infinitely many scaled and shifted Kronecker Only the term for k = n is non-zero, in which case the Kronecker delta is one, so the result is just You can easily see that all terms where k ≠ n are zero, because the Kronecker delta is zero in that case. To prove the previous statement, we'll start with the following trivial property:Īny signal x can be expressed as a convolution of the Kronecker delta function with itself, that is The impulse response describes the behavior of the system, for all possible inputs. The output of discrete-time linear time-invariant (DTLTI) systems, of which the EMA is an example,Ĭan be expressed as the convolution of the input with the impulse response.

įor example, if α = 0.25, the step response is as follows: The Heaviside step function is defined as The step response is the output of the filter when a Heaviside step function is applied to the input. įor example, if α = 0.25, the impulse response is as follows: Y i m p u l s e = h = α ∑ k = 0 n ( 1 − α ) k δ = α ( 1 − α ) n. Recall the definition of the Kronecker delta: The impulse response is the output of the filter when a Kronecker delta function is applied to the input. Y = α x + ( 1 − α ) y = α x + ( 1 − α ) ( α x + ( 1 − α ) y ) = α x + ( 1 − α ) ( α x + ( 1 − α ) ( α x + ( 1 − α ) y ) ) … = α ∑ k = 0 n ( 1 − α ) k x Impulse and step responseįrom the previous equation, we can now easily calculate the impulse and step response. This can be easily demonstrated by substituting the previous outputs: The filter is called 'exponential', because the weighting factor of previous inputs decreases exponentially. If α = 1, the output is just equal to the input, and no filtering
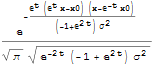
In this equation, y is the current output, y is the previous output, and x is the current The difference equation of an exponential moving average filter is very simple: Plotting the frequency response in Python.Home get_app feedback Exponential Moving Average Pieter P Don't use unions or pointer casts for type punning.Simple Finite Impulse Response Notch Filter.Discretization of a Fourth-Order Butterworth Filter.DTLTI Systems, Transfer Functions, and the Z-transform.Flashing the ESP8266 with an Arduino UNO.Compiling Optiboot - ATmega328P at custom frequency.Configuration options and common use cases.Cross-Compiling the C++ Example Project.Building the Cross-Compilation Toolchain.Ubuntu to Raspberry Pi OS Cross C++ Development.RealDigits can be used to return a list of digits of E and ContinuedFraction to obtain terms of its continued fraction expansion. In fact, calculating the first million decimal digits of E takes only a fraction of a second on a modern desktop computer. E can be evaluated to arbitrary numerical precision using N.Despite its extensive appearance in various closed-form sums and integrals, E is conjectured to not be a Kontsevich –Zagier period (meaning it is not the value of an absolutely convergent integral of any univariate or multivariate rational function with rational coefficients over algebraically-specified domains in ). lt is not known if E is normal (meaning the digits in its base- b expansion are equally distributed) to any base.
However, E is the "least" transcendental number possible since it has irrationality measure of 2. Euler proved that E is irrational (meaning it cannot be expressed as a ratio of any two integers) and Hermite subsequently established that it is transcendental (meaning it is not the root of any integer polynomial).Expansion and simplification of complicated expressions involving E may require use of functions such as FunctionExpand and FullSimplify. When E is used as a symbol, it is propagated as an exact quantity. The exponential function Exp is converted to E^ x.It appears in many sums, products, integrals, in equations involving the compounding of interest, in growth laws involving exponential growth or decay, and in formulas from a wide range of other mathematical and scientific fields. With the possible exception of Pi, E is the most important constant in mathematics. E has a number of equivalent definitions in mathematics, including as the infinite sum of reciprocal factorials over non-negative integers and as the limiting value. It is also known as Euler's number and can be input as \. E is the symbol representing the base of the natural logarithm Log.


 0 kommentar(er)
0 kommentar(er)
